HOME

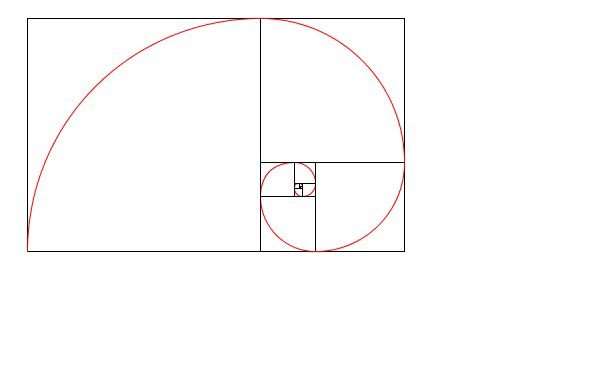
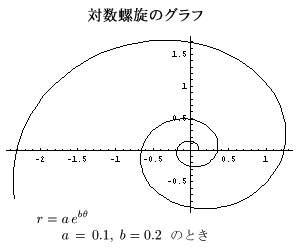
フィボナッチ数列セール螺旋リード角

Name: フィボナッチ数列 セール 螺旋 リード角
Brand: フィボナッチ数列
SKU: C541148624
Price: 15246 JPY
Availability: InStock
Rating: 4.4 (67 reviews)

商品説明・詳細
送料・お届け

商品情報

コラム◇IT散歩／第13回：「『黄金比』・・・その神秘」（後編） - トゥービーソフトジャパン。黄金比。ケプラー三角形，直角二等辺三角形，正三角形等を基準とした楕円に基づく黄金比，白銀比，青銅比，貴金属比，貴金属比の類似比の提案，その連分数と多重根号およびパスカルの三角形，ピタゴラスの定理，桂馬延伸拡張型もしくは一般化されたフィボナッチ数列、リュカ数列と。フィボナッチ数列について（その３）－フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか（自然界以外）－ | ニッセイ基礎研究所。フィボナッチ数列（５）：アルキメデスのらせんと点分布の均一度。3次元フィボナッチ数列黄金比幾何学的形状螺旋カタツムリ螺旋海貝白い円 | プレミアムベクター。フィボナッチ数列による螺旋 - 数学アートの部屋。自然界と人体の神秘～フィボナッチ数列、黄金比から見る～ | フォレスト呼吸器内科クリニック町田 | 町田駅。以前の「ひとこと」2006年5月後半。フィボナッチ的らせん三角形と変拍子について（パドヴァン数列の話） - アジマティクス。

フィボナッチ数列セール螺旋リード角
フィボナッチ数列と黄金比～自然界から金融まで～ | 個別指導のオンライン家庭教師WAM

フィボナッチ数列セール螺旋リード角
コラム◇IT散歩／第13回：「『黄金比』・・・その神秘」（後編） - トゥービーソフトジャパン

フィボナッチ数列セール螺旋リード角
自然界と人体の神秘～フィボナッチ数列、黄金比から見る～ | フォレスト呼吸器内科クリニック町田 | 町田駅

フィボナッチ数列セール螺旋リード角
ケプラー三角形，直角二等辺三角形，正三角形等を基準とした楕円に基づく黄金比，白銀比，青銅比，貴金属比，貴金属比の類似比の提案，その連分数と多重根号およびパスカルの三角形，ピタゴラスの定理，桂馬延伸拡張型もしくは一般化されたフィボナッチ数列、リュカ数列と ...

フィボナッチ数列セール螺旋リード角
コラム◇IT散歩／第13回：「『黄金比』・・・その神秘」（後編） - トゥービーソフトジャパン

フィボナッチ数列セール螺旋リード角
自然界と人体の神秘～フィボナッチ数列、黄金比から見る～ | フォレスト呼吸器内科クリニック町田 | 町田駅

フィボナッチ数列セール螺旋リード角

フィボナッチ数列セール螺旋リード角
フィボナッチ数列について（その２）－フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか（自然界）－ | ニッセイ基礎研究所

フィボナッチ数列セール螺旋リード角
3次元フィボナッチ数列黄金比幾何学的形状螺旋カタツムリ螺旋海貝白い円 | プレミアムベクター

フィボナッチ数列セール螺旋リード角
フィボナッチ数列による螺旋 - 数学アートの部屋

フィボナッチ数列セール螺旋リード角
自然界と人体の神秘～フィボナッチ数列、黄金比から見る～ | フォレスト呼吸器内科クリニック町田 | 町田駅

フィボナッチ数列セール螺旋リード角
黄金角は無数にあった！！～フィボナッチ数列と黄金比から植物の謎に迫る(1) – Taro is here!

残り 8 点 15,246円

（408 ポイント還元！）

翌日お届け可（営業日のみ） ※一部地域を除く

お届け日: 12月18日〜指定可お届け日: (明日15:00のご注文まで)

ラッピング

対応決済方法

クレジットカード
コンビニ前払い決済
代金引換: 商品到着と引き換えにお支払いいただけます。 (送料を含む合計金額が￥281,274 まで対応可能)
ペイジー前払い決済(ATM/ネットバンキング): 以下の金融機関のATM/ネットバンクからお支払い頂けます
みずほ銀行、三菱ＵＦＪ銀行、三井住友銀行
りそな銀行、ゆうちょ銀行、各地方銀行
Amazon Pay(Amazonアカウントでお支払い)